Razor Code

Random number generation seems to be an often used example of where functional programming falls down. The argument is that you need the random number generator to return a new result every time you call it. To do that, it either needs internal state (so it is not pure) or the current state must be carefully threaded through the entire program. Passing that state in and out of every function is clearly going to ruin your beautiful design. James Hague, who I greatly respect, lists this as one of the reasons that functional programming doesn't work. I hope to convince you that everyone has been doing random number generation wrong, and a more functional approach to it would benefit old fashioned imperative programmers too.

Pure random numbers

Generating pseudo random numbers in a pure, side effect free way is not a problem. I'll provide real Haskell source code at the end, but the basic idea is to define an infinite list where each item is defined in terms of the previous item, except the first item which is the seed. If you aren’t used to infinite lists, just think of this function:

  int random(int seed, int index) {
        if (index == 0) {
            return seed;
        } else {
            return scramble(random(seed, index - 1));
        }
    }

where scramble is the typical bit twiddling to generate the next number. The result of this function depends only on the inputs given, so it meets our purity requirement. However, it means we have to keep track of which index we are up to. Keeping track of state like this across almost entirely unrelated parts of the program, passing it in and out of every function, is exactly what we wanted to avoid. What else can we do?

More generators

Perhaps we could improve this a bit by using separate random number generators in different modules of the program. We can initialize them with different seeds and get multiple independent streams of random numbers, slightly reducing our horrible tangle. So far so good, but what we really want is an arbitrary number of random number generators where the exact number of generators is determined at runtime. I want to be able to define a rock which uses a random number generator to determine it’s shape, and I want to define a world with an arbitrary number or rocks. So how do we seed all these generators? We use a random number generator, of course!

Number trees

Programs are tree structured. If I am building a game, my level might have a baddie, and that baddie might have a weapon, that weapon might emit shell casings, those shell casings might make a sound. We break our programs down in this tree structured way in order to deal with their complexity. I think it is fair to say that all large programs are like this, they may not be object oriented, but they still compose their functionality from smaller pieces. So why don't we build a tree of random numbers instead of a list? All we need is the ability to seed a random number generator using a previously generated number, and have it produce something other than the next number in the sequence of the original generator. If you recall the scramble function from earlier, all we need is a second, different scramble function. Imagine a tree where scramble1 produces the left child, and scramble2 produces the right child.

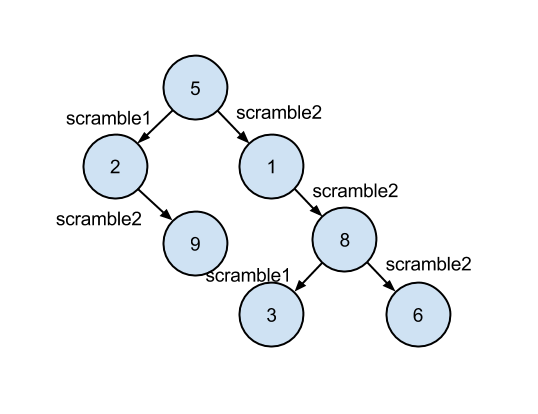
Examples

Now we can build some clean programs. Lets say I want to generate a level with 5 baddies.

  level seed = map baddie (take 5 (random seed))

Or if you prefer the C++ version:

  vector<Baddie*> level(int seed) {
        vector<Baddie*> baddies;
        for (int i = 0; i < 5; i++) {
            baddies.push_back(new Baddie(random(seed, i)));
        }
        return baddies;
    }

And our baddie can use as many random numbers as needed:

  baddie seed = (color (rand :: 0), weapon (rand :: 1))
        where
            rand = random seed

Or in C++:

  Baddie(int seed) {
        this.color = random(seed, 0);
        this.weapon = new Weapon(random(seed, 1));
    }

If something requires random numbers, you pass it a seed. Simple. Conceptually, any function (or object) which calls a function which uses a random number generator is itself random to some degree. So it makes sense that we pass a seed in, because it gives us control over the randomness in this function or object in a simple way. If we pass the same seed, we get the same result. As we all know, randomness is too important to be left to chance.

Benefits

By building a tree of random numbers to match the tree structure of our program, we can now control those numbers at any level. If some user setting means the baddie requires an extra random number, it only affects that baddie, not every other object. If you use something like the C rand() function, reading one extra number will change every number that is generated after it. Now it only affects one branch of the tree. This opens up new possibilities. Suddenly you don't have to store all your random numbers, you can rely on the same seed producing the same numbers instead. There is no magic hidden state that could have been trashed in the mean time. And you can put all of that into practice without using a functional language. It feels strange, almost wrong that these deterministic sequences have always been hidden behind stateful functions.

Haskell Mersenne Twister

As promised, here is my pure Haskell Mersenne Twister implementation, based on the Wikipedia pseudo code and checked against the 200 numbers listed here. Ironically, this generator is not well suited to the tree like number generation I spent most of this article advocating. The reason is it will churn through 624 iterations before it gives you your first number from a new seed. I haven't written an RNG suited to generating trees of numbers, because I don't know how. I'm also not very good with Haskell, so please bear with me while I fail all over the internet.

  module Main where
    
    import Data.Word
    import Data.Bits
    
    -- An infinite list of tempered pseudorandom numbers.
    mersenneWords :: Word32 -> [Word32]
    mersenneWords seed = map temper (untempered seed)
        where
            temper x =
                let y1 = x `xor` (x `shiftR` 11)
                    y2 = y1 `xor` ((y1 `shiftL` 7) .&. 2636928640)
                    y3 = y2 `xor` ((y2 `shiftL` 15) .&. 4022730752)
                    y4 = y3 `xor` (y3 `shiftR` 18) in
                    y4
    
    -- Untempered numbers, where each number is generated using 3 previous numbers in the list.
    untempered :: Word32 -> [Word32]
    untempered seed = zipWith3 genNum self (tail self) (drop 397 self)
        where
            self = initialState seed ++ untempered seed
            -- Generate a new number using a, b and c.
            -- a is 624 numbers ago, b is 623 numbers ago and c is 227 (624 - 397) numbers ago.
            genNum a b c = if even y then evenResult else evenResult `xor` 2567483615
                where
                    y = (a .&. bit 31) + (b `clearBit` 31)
                    evenResult = c `xor` (y `shiftR` 1)
    
    initialState :: Word32 -> [Word32]
    initialState seed = take 624 initialValues
        where
            initialValues = seed : zipWith genNextValue [1,2..] initialValues
            genNextValue i prev = 1812433253 * (prev `xor` (prev `shiftR` 30)) + i
    
    main = print $ take 200 $ mersenneWords 1