Razor Code

A couple of years ago, I had an idea for planning paths for wheeled robotic vehicles. Self driving car type vehicles with normal steering (non-holonomic). I thought a cheap heuristic which guides the search around obstacles but still underestimates would make it possible to find paths which were close to optimal in reasonable time. I got as far as writing a test app for it, and it seemed to work exceptionally well, so I did what anyone would do in that situation; I left it stagnating on my various hard drives. It could be useful in robotics or game development.

Disclaimer: I am an arm-chair robotics engineer, it is quite likely that my ideas are well known, terrible or perhaps both. I have not done my research, and this is not my job. Not any more, anyway.

The Problem

When planning a path for something like a car, the properties of the vehicle are very important. There will be paths you cannot take because the turning circle is not small enough. When looking for the fastest path, it may be faster to take a longer route because it is straighter and speed must be limited while turning. There may be a limit to how close the vehicle can come to obstacles at speed. All of that means you want to do your planning at the granularity of changes to the vehicle controls. If you don't know exactly what all of your speed and steering angle changes will be, you can't really claim to have found a path, let alone the best one.

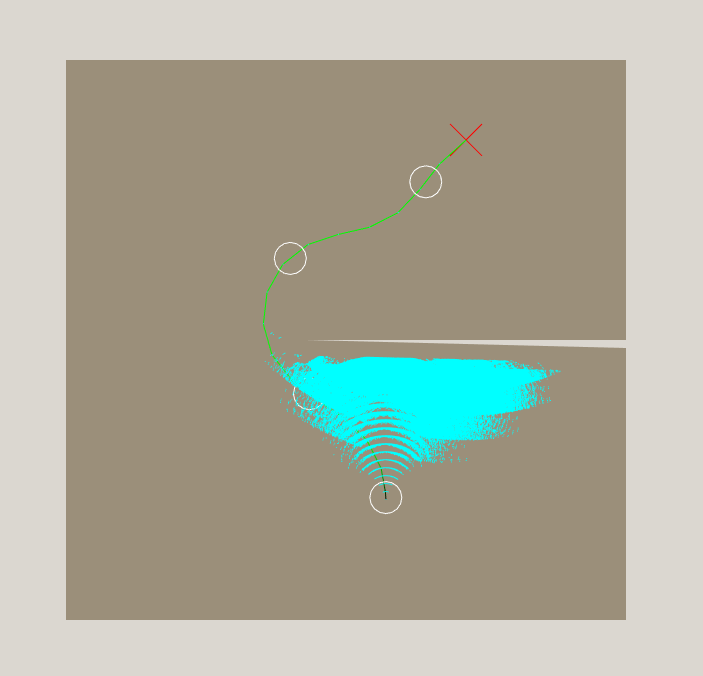
But there is a problem: For any remotely interesting map, the search space of possible vehicle control changes is large. Very large. Of course, if you use A*, you don't have to expand the whole search space. A simple heuristic like distance-to-goal can cut down the search time quite a bit, but it falls over in some very common situations. Imagine your vehicle and the goal are sitting either side of a wall, as shown below. Distance-to-goal will try every possible way of crashing into the wall before it finds the way around, because positions close to the wall have much more promising heuristic values than positions around the ends.

Multilevel path planning

If only we could plan a rough way of getting from A to B, then refine it afterwards taking our vehicle characteristics into account. Say you are planning a path through a house, you might decide which rooms you are going to pass through first, then use do your refined search with the heuristic of how close you are to the next room (roughly speaking). This works (probably) but it bothers me for a couple of reasons:

• There are two kinds of rough paths, those that include impossible paths and those that exclude possible paths.
• Your heuristic is probably not always less than the shortest real path to the goal anymore, so optimality goes out the window (definitely if you only planned one rough path and there are multiple ways of getting to the goal).

Perhaps my distaste was not so much about the idea of multilevel path planning, but the very approximate, ad hoc approaches to it that I was seeing. It always seemed to start with "divide your world into a regular grid" and only get worse from there.

Non-colliding distance heuristic

It is clear we need a better heuristic which will direct the search around obstacles, but I'm not happy with planning an approximate route in advance. I want a heuristic that:

1. Always underestimates, which is required for optimality. Even if we don't need the optimal path, it is nice to know how far off it could be.
2. Directs the search around obstacles, so the search only has to deal with the fine details of control.
3. Is quick to compute, because while I don't want to expand a lot of the search space, it is nice to be able to.

What if we could find the shortest path from the current vehicle location to the goal which does not pass through any walls or obstacles, ignoring the turning/acceleration characteristics of the vehicle? Or, put simply, find the time it would take the vehicle to reach the goal if it always traveled at full speed and could turn instantly on the spot. For the starting position, that would look something like this:

We want to evaluate that cost for every one of the hundreds of thousands (millions?) of nodes that are expanded during the search. Sounds expensive. But notice how the line always seems to go from corner to corner of the polygon. It seems like there should be large areas of the polygon where the shortest path always goes to a particular corner first. After hitting that corner, the path to the goal will always be the same. If we can find those areas, we can compute this heuristic quickly.

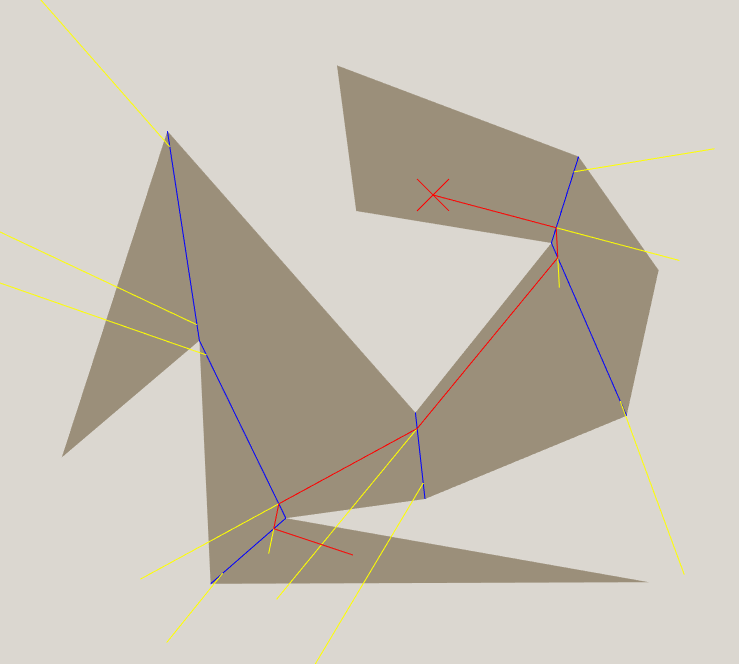
We will start by dividing the polygon into convex polygons, with the shared edges shown in blue (I call them portals).

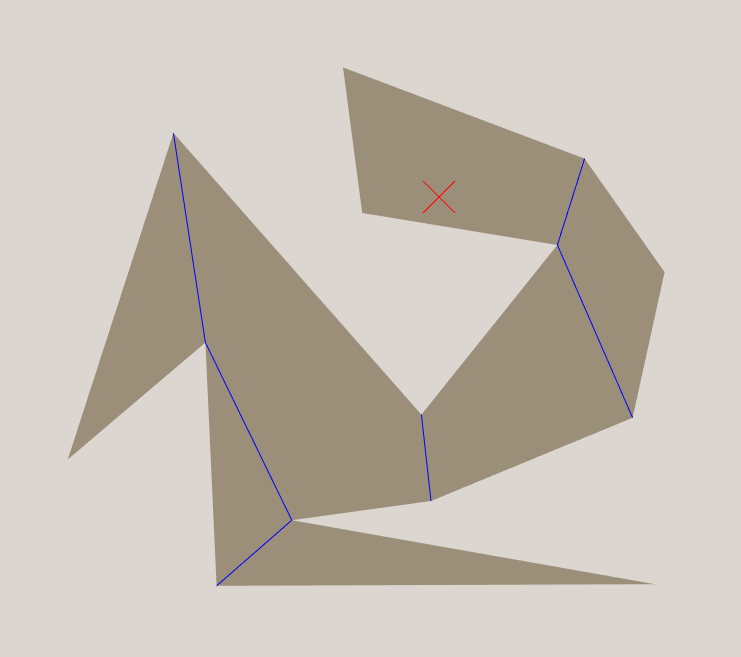
Now, within the goal zone (red X shown), the non-colliding distance will always be the straight line distance to the goal. If we are on the other side of the nearest portal, there are two possibilities. If we are in the top part of the zone, the non-colliding path will be straight through the portal to the goal. If we are in the bottom part of the zone, the non colliding path will go up to the corner of the portal, then straight to the goal.

In the general case, to calculate the distance to a goal using a particular portal, there are 3 possibilities:

1. Distance to first corner + distance from first corner to goal, calculated using next portal
2. Distance to second corner + distance from second corner to goal, calculated using next portal
3. Distance to goal, calculated using next portal

For the purposes of this algorithm, a goal can be considered a 0 sized portal.

I will show the regions for each portal in yellow.

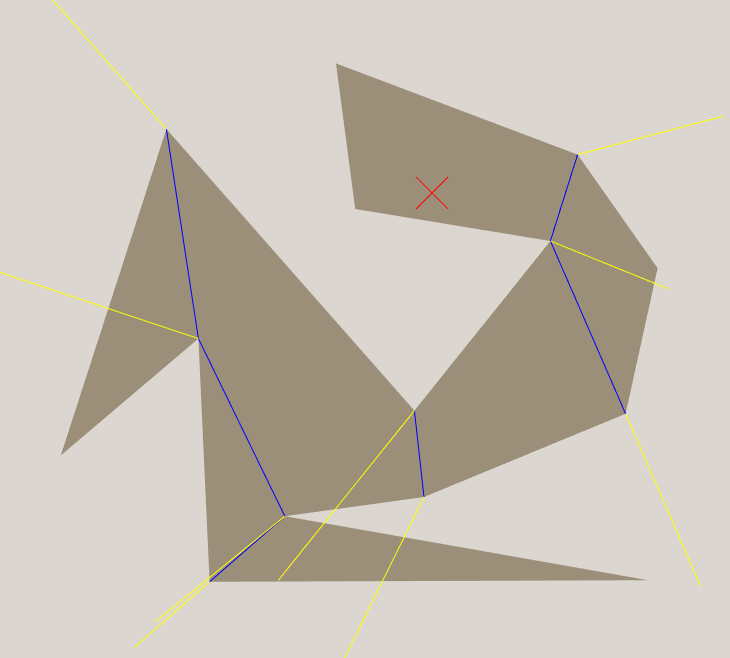
We can pre-calculate the distance from every portal corner to the goal, and since they only depend on the goal location, we can keep reusing them throughout the search. I have not yet implemented obstacles in the map, but if I did there would still only be one shortest path from each portal corner to the goal. The only increased complexity would be that in some zones you would have to apply the heuristic to multiple portals and take the best outcome.

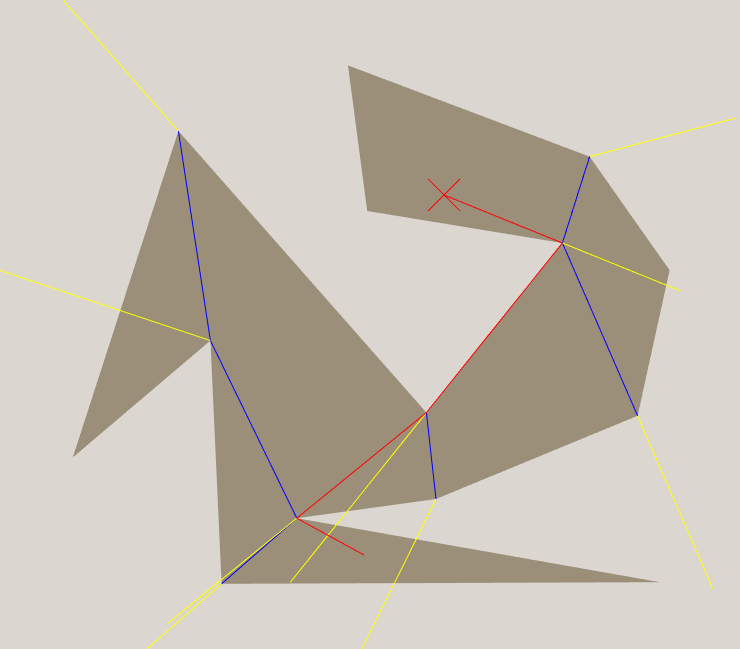
This heuristic is very cheap. Each node we expand will generally be in the same zone as the previous node, and we can check if the vehicle has left the zone as part of our collision detection. Generally we only have to check one or two portals before we find the portal corner we should use to calculate the heuristic. Each portal takes two dot products to determine which region we are in, and once we find the appropriate portal corner, it is just straight line distance plus a constant. The expensive part is probably the square root, which makes it barely more expensive than straight line distance!

Trying this on my first example, we get much better results.

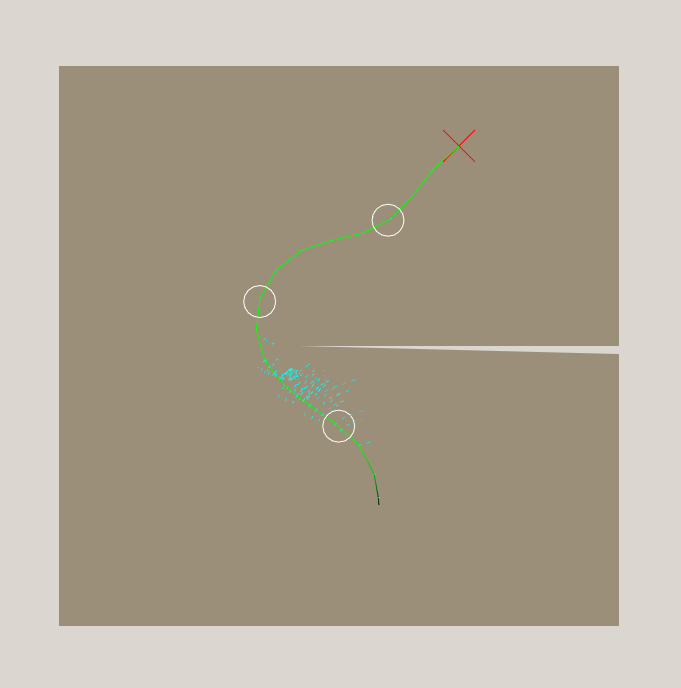
The Vehicle Model

If you use this heuristic with a very simple vehicle model and the tricks I describe later, it is pretty easy to get your search done in ~0.02s, expanding 500-1000 nodes. This happens because the heuristic is so close to the actual path that the search barely backtracks. That might be useful for some games, but I wanted something more realistic, something that would produce smooth, drivable paths, slowing down for sharp corners and keeping away from obstacles when moving fast. It didn't have to be physically accurate, just somewhat believable, to stretch the planner a bit. This is what I came up with:

• 3 Speeds, 0, 10 or 20 pixels per timestep.
• Accelerating/decelerating takes one timestep, so if you decide to accelerate your average speed for that timestep will be halfway between your previous and target speeds.
• Collision radius of 10 pixels, with a safety zone of an extra 5 pixels at speed 1 and 10 pixels at speed 2.
• Wheel base of 10 pixels.
• Maximum steering angle of +-33.75 degrees, split into 3 steps of 11.25 degrees (1/32 of a circle).
• Incrementing/decrementing steering angle takes one timestep, so your average steering angle for a timestep may be halfway between these values. The steering angle can be changed while stationary, but it won't rotate the vehicle, obviously.
• Maximum steering angle at speed 2 is +-11.25 degrees. At speed 1 the full range of steering is available.

The safety zone and speed dependent steering angle are actually really tough conditions. When faced with the ability to go fast or go the right direction but not both, many search algorithms get kind of stuck.

Tricks for Speed

The vehicle model above is very ambitious. How ambitious? Well, it has been running for over 40 minutes on a fairly simple map and it hasn't found the optimal path yet. I'm not sure it ever will, so I'm going to stop it there. That's disappointing, but I still have a couple of tricks up my sleeve.

Foregoing Optimality

I don't really need the perfect path, the vehicle model is an approximation anyway. I would probably satisfied knowing my path was not more than 50% slower than the optimal. We can do this by adjusting our A* heuristic, and it is called bounded relaxation. Normally the next node to expand is the one where travelled time + heuristic time is lowest. If we ignored travelled time and only considered heuristic time we would have a greedy algorithm, and the found path would look like this:

I actually cheated a bit on this one, with a true greedy algorithm the oscillations get so bad that it doesn't find the goal in any reasonable amount of time. The sweet spot is somewhere in between greedy and optimal. We want to give up on paths that aren't turning out as promising as they once looked, which greedy doesn't do. And we don't want to spend all of our time fussing around the start location just because it had promising heuristic values, which we would do if we were going for optimality.

My current favourite weighting is to find a path within 20% of optimality. That is, if I am going to expand a node at the start because it has a low heuristic value, that value needs to be at least 20% lower than the actual travelled distance of a node near the goal. Here are the results:

Search completed in 12s after expanding 735116 nodes. Now we are getting somewhere! The path looks short and smooth, and the search completes in a reasonable amount of time. It still isn't fast, though. Not the kind of thing you would want to update on the fly, or plan for multiple vehicles simultaneously.

Adjusting for vehicle size

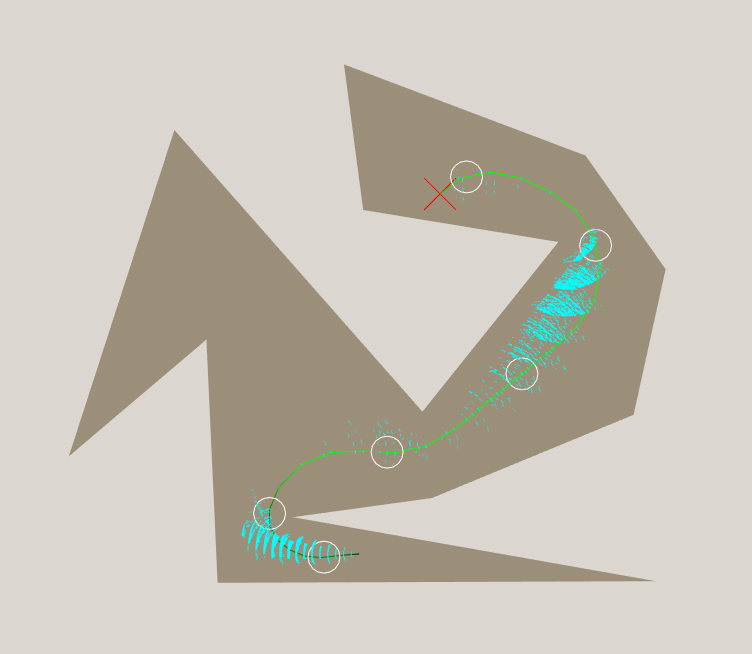
Fear not, though, I have one trick left. But first, how about we take a look at the closed list of the search. I will draw a tiny blue dash at each position that was expanded.

Wow. That is a lot of expanded nodes. Everything it tried was in the general direction of the goal, so my heuristic is working to some degree, but it looks like the actual path is much more than 20% longer than the heuristic, so it had to expand a heap of nodes before it could be sure that the path was within 20% of optimal. You can see this in the numbers, too. The path was 30 timesteps long, and the heuristic at the start node claimed 18.4 timesteps. It expanded so many nodes that I wouldn't be surprised if the path was within 1% of optimal in practice. So, shall we relax the 20% constraint? No, because I have a better idea: Bring the heuristic closer to the truth.

The non-colliding distance hugs the walls and corners much closer than we have any hope of doing with the actual vehicle, so it underestimates quite badly. We can push it away from the walls by the radius of our vehicle and it will still be provably shorter than the shortest real path, so we can still make claims about optimality. If your vehicle is not circular (hardly surprising) you can just take the largest circle entirely contained within the vehicle, or if there is a minimum distance you must maintain from obstacles, you can use that. All you have to do is shrink your portals by that radius, as shown:

This gives us an estimate from the start node of 20.16 timesteps. So what, right? That is barely any different to the 18.4 we had before. Well, let's try it:

Search completed in 0.44s, expanded 24326 nodes, and the resulting plan is still 30 timesteps. Notice how the closed list is way more reasonable than before. A good heuristic is a powerful thing. I believe the reason it is so much faster is because the heuristic directs the search more toward the next portal, where previously it directed the search into the wall.

Speed/Optimality tradeoff

You might be wondering "why 20% relaxation"? That is a fair question. The value that works for you will depend on how tricky your search is. In general, the trickier your search, the less accurate your heuristic, and the more you have to relax your bound. You may also choose to relax it if you have strict time constraints, but don't go too far or it will end up slower!

Lets try some values. I made the timestep a bit smaller for this table because otherwise you could barely see the difference. I haven't got a good way of measuring partial timesteps.

% relaxation	Time (s)	Path length (timesteps)	Expanded nodes
15	28.528	38	1614389
20	2.650	38	171882
30	0.840	38	59262
50	0.490	39	31301
100	0.089	44	6262
200	0.004	54	453
400	0.002	61	270
800	0.011	89	775
1600	0.043	72	3290

Conclusion

You should totally try out this heuristic.

Future work

• I haven't dealt with orientation or speed at the goal location, I just decided near enough was good enough. If I was going to do this I would attempt a heuristic which was something like half a dubins path, so it takes into account orientation of the goal but not the vehicle.
• I haven't implemented obstacles. This would require some updates to the heuristic calculation.
• The planning results in many nodes which are incredibly close, but not exactly the same. I have ignored this problem because I figured any complex vehicle model would have a roughly infinite search space anyway. Combining nodes within a certain margin of error would probably speed up the search.
• It would be interesting to plan for more than one vehicle at once.
• Rather than picking a relaxation level, it would be interesting to search with multiple relaxation levels at once. In theory, this could turn out better than any one relaxation level because (for example) your greedy search would go straight for the goal from the best node found by any of the searches, so it wouldn't get so stuck. As soon as any search reaches the goal you can stop any search more relaxed than it, so you don't waste your time with the last couple of entries in the tradeoff table. It would probably require multiple priority queues.